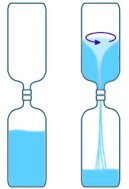
Water Vortex
There are several ways to demonstrate the motion of a vortex. The most simple method would be the popular vortex in a bottle type. This can be made by sticking two plastic bottles end to end by their lids. With a hole through the adjoining lids water can be made to pass from one bottle to the other, under the influence of gravity. A simple swirl of the bottle is enough to make the water spin and accelerate to form a vortex.
Vortex Cooling
A vortex tube is a method commonly used for cooling. By forcing compressed air into the device vortices will form which allow hot air to exit from one end whilst the cold dense air exits the other end.
Info from Wikipedia
The vortex tube, also known as the Ranque-Hilsch vortex tube, is a heat pump with no moving parts. Pressurized gas is injected into a specially designed chamber. The chamber’s internal shape, combined with the pressure, accelerates the gas to a high rate of rotation (over 1,000,000 rpm). The gas is split into two streams, one giving kinetic energy to the other, and resulting in separate flows of hot and cold gases.
The vortex tube was invented in 1930 by French physicist Georges J. Ranque. German physicist Rudolf Hilsch improved the design and published a widely read paper in 1945 on the device, which he called a Wirbelröhre (literally, vortex tube).
Vortex tubes have lower efficiency than traditional air conditioning equipment. They are commonly used for inexpensive spot cooling, when compressed air is available. Commercial models are designed for industrial applications to produce a temperature drop of about 80 °F (45 °C).
Another application is for uranium enrichment. South Africa used vortex tubes in their Helikon vortex separation process.
Dave Williams, of Engineers Without Borders, has proposed using vortex tubes to make ice in third-world countries. Although the technique is inefficient, Williams hopes it could yield helpful results in areas where using electricity to create ice is really not an option.
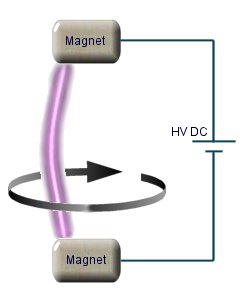Plasma Vortex
A plasma vortex can be made through the interaction of electric and magnetic fields. A simple setup in a homemade vacuum chamber allows a plasma column to form within the magnetic field of a pair of rare earth magnets. The plasma column will rotate around the magnets in a direction which depends upon the polarity of the fields.
Any literature citations or references that give details on how to produce a plasma vortex using magnets? I am speaking of nuts-and-bolts info, that will allow one to do the experiment. details, materials, dimentions, magnet strengths, etc. Thanks for your time.
I don’t know. I suspect it would be calculated based on the dimensions and the gas pressures.
How did they come up with the 1 Million RPM number? Was it by experiment or mathematics? I am looking for a somewhat detailed answer. I’m in a freeze seal class where we get to learn to use the vortex tubes to freeze pipes for industrial purposes and it is very interesting.
Mercury is not a ferrofluid.
Spinning a substance would only change its specific gravity (relative density) if the centripetal forces were sufficient to cause pressure changes.
can you vortex a ferrofluid like mercury and get it spinning at a high enough rate to change specific gravity of the vortex
Check out this massive vortex cannon from the BBC.
In vortex tube has possible to seprate nitrogen and oxygen
1. They don’t increase resistance or the length of the arc. The flow of current is just guided by the field lines.
2. No
1: is the magnet affecting the resistance with more of an effect then just increasing the length of the arc?
2: if the magnets were rings would the plasma take a coil shape instead of just avoiding the magnets fields?
It needs to be a compressible fluid or something which can have density gradient within it. It may be possible with liquid mixtures or solutions where the components of the liquid are of different molecular masses.
Magnetic fields could cause vorticies of charged particles if they are moving like shown above.
Does it matter what type of gas you use?
Can liquid be used instead of gas?
Can anything that has a pressurized flow be split into two streams similar to compressed air?
Is there an equivalent way to split electrical pressure into two streams? And what might an electrical vortex tube look like?
Does it Matter Which Way the Magnets Are Facing?
The magnets are arranged so that they are attracting eachother with the poles pointing parralel to the electric current.
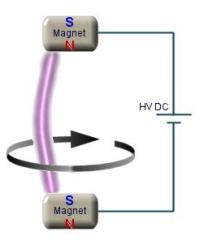
it is the magnetic field produced by the current flowing in the arc which reacts against the field of the magnets.
It would probably interupt the cooling effects, but it would be possible to generate power this way.
It is unlikley though that it would be a particulary efficient way to convert the energy in compressed air into electricity.
I wish i was a scientist. I had an idea but I dont know if it would work. In the vortex cooling part, it mentions that you get an rpm of over 1,000,000. Could a fan be placed inside connected to a turbine/dynamo to provide electricity? If it could, would it be efficient? If anyone knows anything about this please could you do some experiments.